레이블이 정확하지 않을 때, 이렇게 하세요

Learning with Noisy Labels

기계학습에 공급되는 레이블은 대체로 누군가의 고된 노동으로 마련됩니다. 워낙 재미는 없는데 집중력은 필요한 작업이다 보니 디지털 시대의 곰 눈 붙이기라고 부르기도 합니다. 작업 단가를 낮추기 위해서 얼굴 모르는 사람에게 아웃소싱을 주는 플랫폼도 많이 사용합니다. 그런데 이런 식으로 수집된 레이블이 결과물이 백퍼센트 올바를까요? 인터넷을 통해서 대량으로 다운로드받을 수 있는 데이터셋을 이용하는 경우도 있지요. 그 경우도 안심할 수 있을까요? 누가 오류가 있는 레이블만 따로 모아준다면, 그것만 다시 올바르게 레이블링 하겠지만, 수많은 레이블 중에서 어디가 틀려있는지 찾는건 만만치 않습니다. 전체를 재검토할 시간에 새로운 레이블을 그냥 계속 더 만들어내는게 비용상 효율적일 수 있습니다. 그렇다면 발상을 바꿔서, 레이블에 어느정도의 오류가 있다는 것을 인정하고, 오류가 있더라도 트레이닝이 결과적으로 잘 되는 방법이 없을까요? 이번 글에선 이런 문제의식에서 나온 연구들을 살펴보겠습니다.

오류가 있는 레이블들은 더티 셋 dirty set 이라 합니다. 오류가 없는 레이블들은 클린 셋 clean set이라 합니다. 이 분야 연구들은 주로 이 두 레이블 집합의 트레이닝 과정 중에 나타나는 차이에 대해서 관찰하고, 나름의 가설에 따라서 해결책을 제시합니다.

---

Decoupling “when to update” from “how to update”
Malach and Shalev-Shwartz, 2017 [arxiv]

비유를 들어 봅시다. 문제집을 푸는데, 답안지에 대한 신뢰가 좀 떨어지는 상황이라고 합시다. 성적이 상위권인 삼식이와 삼순이가 각각 문제를 풀어서 답안지와 대조해 봅니다. 13번 문제는 답안지에는 정답이 3이라고 되어 있지만, 삼식이와 삼순이는 둘 다 5라고 썼습니다. 답안지에 오류가 있다고 했는데, 그럼 이 13번 문제는 답안지가 틀린 것이 아닐까 의심해볼 수 있습니다. 이럴 때, 삼식이와 삼순이는 둘이 함께 같은 내용으로 대답한 문제는 더 공부할 필요가 없는 것으로 간주하고, 둘의 응답이 엇갈린 문제만 집중해서 공부하기로 합니다.

아래 알고리즘은 지금까지 얘기한 비유를 다른 말로 표현한 것입니다.

---

Co-teaching: Robust training of deep neural networks with extremely noisy labels
Han et al., 2018 [arxiv]

삼식이가 문제집을 풉니다. 문제 100개를 풀었습니다. 채점을 하기 전에, 풀었던 문제들에 대해서 각각 얼마나 확신하는지 삼식이한테 물어봅니다. 어떤 문제는 맞출 자신이 있다고 말하고 어떤 문제는 잘은 모르겠다고 말하겠지요. 이 중 가장 자신이 없는 문제 순으로 10개는 제외하고 90개의 문제에 대해서 답안과 대조를 하고 채점을 해서 학습을 합니다.

답안지에 약간의 오류가 있는 경우에는 이 방법이 효과가 있습니다. 같은 문제집을 여러 번 풀면서 (에포크라고 부릅니다) 점차 학습을 해 나가는 과정에서, 답안지에 오류가 있으면 삼식이가 답안지와 다른 답을 낼 확률이 높습니다. 오답을 기록한 문제는 학습과정에서 조금씩 답안지가 요구하는 결론으로 응답을 바꾸게 되는데, 그 과정에서 필연적으로 예측에 대한 확신이 떨어지는 때가 옵니다. 이렇게 학습자에게 확신이 적은 문항은 답안지가 틀렸을 확률이 높은 것으로 간주하고 학습에서 제외하는 것입니다. 이 방법은 small loss selection이라 부릅니다.

하지만 이 방법에는 문제가 있습니다. 삼식이에게 무슨 문제를 빼고 싶냐고 물어보는 셈이 되기 때문에, 배우기 까다로운 문제는 자신이 없다고 말하고 빼버리는 수가 있지요. 성적이 아주 하위권이라면 대세에 상관이 없고, 이게 오히려 더 효율적인 학습전략일 수 있습니다. 하지만 일정 수준 이상의 성적을 거두고 나면, 배우기 어려운 부분은 영영 빼버리고 만만한 문제만 풀기 때문에 성적이 오르는 데 한계가 뚜렷하겠죠.

전략을 조금 바꿔 보겠습니다. 두 명이 공부를 하는 겁니다. 삼식이와 삼순이가 같은 문제 100개를 각자 풉니다. 삼식이에게 가장 확신이 없는 문제 10개를 제외하고 90개의 문제를 뽑습니다. (삼식이가 아니라) 삼순이는 그 90개의 문제를 답안지와 자신의 풀이를 대조해 보고 학습을 합니다. 이번엔 반대로 삼순이에게 가장 확신이 없는 문제 10개를 제외하고 90개의 문제를 뽑습니다. 삼식이는 그 90개의 문제를 답안지와 자신의 풀이를 대조해 보고 학습을 합니다. 이렇게 하면 내가 어렵다고 생각하는걸 내 학습에서 제외하는 것을 막을 수 있습니다. 나는 남이 어렵다고 생각하는걸 빼고 풀게 되거든요.

[참고] 비유로 든 문제풀이에서 삼식이가 풀이에 대해 얼마나 자신있는지는, 기계학습 용어로 confidence에 가깝긴 합니다. 논문에서 언급하는 로스와 기술적으로는 차이가 있습니다. 이해를 돕기 위한 비유이니, 어떤 원리로 작동하는지 알게 되었다면 그것으로 비유의 목적을 달성한다고 생각합니다.

---

Early-Learning Regularization Prevents Memorization of Noisy Labels
Liu et al., 2020 [arxiv]

아래에 소개된 가 이 연구에서 제안하는 로스입니다.

는 분류기(classifier)에서 흔히 사용하는 크로스 엔트로피 로스입니다. 원래 다들 하고 있는 것이니 특별할 게 없습니다. 이 연구에서는 두번째 항을 추가한 것이 핵심인데요. 찬찬히 살펴보겠습니다. 은 미니뱃치 안에 들어간 데이터 갯수고, 는 와 균형을 맞추려고 넣은 가중값입니다. 는 트레이닝 중이던 신경망이 데이터 에 대해서 산출한 예측값이고, 트레이닝 과정에서 변화해온 값들을 평균해서 산출한 것이 입니다. < , > 모양은 벡터의 내적을 뜻합니다.

이게 다에요. 구현도 간단하고 계산도 빠릅니다. 트레이닝 셋의 데이터 각각에 대해서 값만 추가로 더 저장하고 있으면 됩니다. 이 로스를 사용하면 레이블에 노이즈가 있어도 트레이닝이 효과적으로 된다고 합니다. 다시한번 식을 잘 보세요. 정말 그래 보이나요? 사실 저는 “어째서?” 라는 의문이 금방 해결되지는 않았습니다.

식 안에 숨어있는 함의를 좀 더 숙고해 봅시다. 는 소프트맥스를 거쳐서 나온 값입니다. 그러므로 벡터의 각 원소의 합은 1로 맞춰져 있습니다. 고양이인지 강아지인지 맞추는 분류기인 경우, 예컨대 이렇게 고양이일 확률 0.8, 강아지일 확률 0.2로 해석할 수 있습니다. 발생할 수 있는 값은 아래 그림처럼 직선 위에 나타납니다.

는 트레이닝 과정에서 변해온 의 평균이라고 했습니다. 짧게 말해 예전 값입니다. 예컨대 라고 해 봅시다. 가장 최근의 값인 이 위 그림처럼 가 나왔다고 하면, 입니다.

다른 예로 위 그림처럼 인 경우에는 입니다. 보셨나요? 과거의 값들에 비해서 최근 예측값 이 더 치우친 예측을 할 때 (고양이일 확률 0.8로 더 강한 확신을 보일 때), 내적은 더 큰 값을 산출하고, 이는 전체 로스를 더 낮추는 기울기를 만들어냅니다.

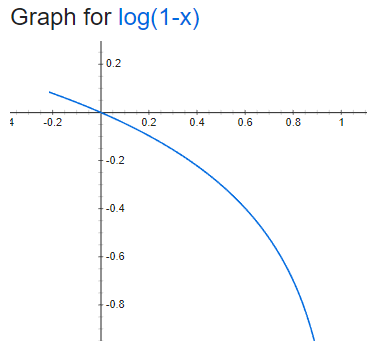
이게 레이블 노이즈와 관련있는 이유는 이렇습니다. 학습 초기에는 어느 한 쪽으로 치우친 예측이 나오기 어렵습니다. 학습이 중간쯤 진행되었다고 해보면, 예측에 자신감이 생기면서 그에 따라 좀 더 분명한(치우친) 예측값이 나오겠죠. 레이블에 노이즈가 있는 경우에는 적당히 트레이닝된 신경망은 예측값과 레이블이 서로 다를 확률이 높습니다. 이러면 크로스 엔트로피 로스 에 따라서 예측값이 레이블 쪽으로 이동하려고 하겠죠. 하지만 이미 한번 치우쳐버린 예측값을 되돌리려면 로스를 많이 높이게 됩니다. 위의 log(1-x)그래프를 보면 1에 가까워질 수록 빠져나오기 힘든 수렁으로 들어가는걸 보실 수 있습니다. 다시 말해 한 번 고양이인것 같다고 추측하기 시작했으면, 기존 추측을 강화하는 쪽으로 변하는 것이 유리하지, 다시 예측을 바꿔서 강아지일 확률이 더 높다고 하기는 힘들어지는 겁니다. 이 원리로 신경망이 원래의 예측을 번복하고 잘못된 레이블을 따라가는 것을 방지하게 됩니다.

---

ProMix: Combating Label Noise via Maximizing Clean Sample Utility
Wang et al., 2022 [arxiv]

이번 연구에서는 먼저, 앞서 소개했던 small-loss selection을 수행해서 일차로 클린 셋을 뽑아냅니다 (논문의 3절 CSS와 MHCS를 참고). 이 방법은 확신이 없다고 응답한 문항은 답안이 올바르더라도 안 배워버리는 문제가 있다고 했습니다. 달리 말하면 로스가 큰 것으로 분류된 쪽에 여전히 클린 셋과 더티 셋이 섞여있다는 뜻이죠. 이제 이 글의 맨 처음에 소개한 [Malach and Shalev-Shwartz, 2017]의 방법을 사용해서 다시한번 클린 셋을 걸러냅니다. 신경망 두 개를 트레이닝하면서 둘의 예측값이 일치하는 데이터는 레이블이 올바르다고 간주하는 겁니다. 아래 그림에서 빨간 공은 더티 데이터와 클린 데이터가 섞여있는, 노이지 셋을 나타냅니다. 어떻게 분류가 되어가는지 살펴보시기 바랍니다.

마른 걸레도 짜겠다는 각오로 클린 셋을 꾹꾹 짜냈습니다. 이러고 남은 더티 셋은 레이블이 없는 것으로 간주해서 세미 수퍼바이즈드 러닝(SSL)을 수행합니다. 버리는게 하나도 없어요. SSL로는 mixup, consistency regulation과 같은 기존에 소개되어 있던 방법을 동원합니다. 위 그림의 회색 상자 부분에 해당합니다. 각각에 대해서 상세하게 다루지는 않겠습니다.

이 논문은 배경이 되는 연구에 대해서 알고 있다면 읽기에 평이합니다. 다만 이걸 따라 구현해서 내 프로젝트에 활용하기에 유리하지는 않은 것 같습니다. 데이터를 분류하는 과정에서 임시로 신경망을 훈련하는 과정도 들어가고, 여러 모듈이 모여서 작동하므로 코드도 심플하지는 않아 보입니다. 그럼에도 온갖 기존 기술을 총동원해서 끝까지 데이터를 활용해 내는 정성이 중요한 것 같습니다. 이 연구는 2022년 현재 여러 벤치마크에서 가장 우수한 성과를 거두고 있습니다.

온스퀘어에서는 소프트웨어 개발자를 상시 채용하고 있습니다.